(SGBD) FUNCIONALES

(SGBD) FUNCIONALES

Las variables funcionales se caracterizan por la evolución de una variable a lo largo del tiempo (proceso estocástico), de modo que los valores que toman son funciones en lugar de  vectores como en análisis multivariante clásico. La imposibilidad de medir la mayoría de estas variables continuamente en el tiempo, unida a la complejidad teórica de muchos de los métodos estadísticos disponibles para su análisis llevan a que se manejen resúmenes periódicos que constituyen las series temporales contenidas normalmente en los anuarios estadísticos. Aunque existen muchas técnicas para la modelización y predicción de datos temporales discretos, la mayoría de ellas, como por ejemplo la teoría clásica de Box-Jenkins, imponen que se verifiquen hipótesis bastante restrictivas como estacionariedad, observaciones igualmente espaciadas o pertenencia a una clase de procesos específica. 

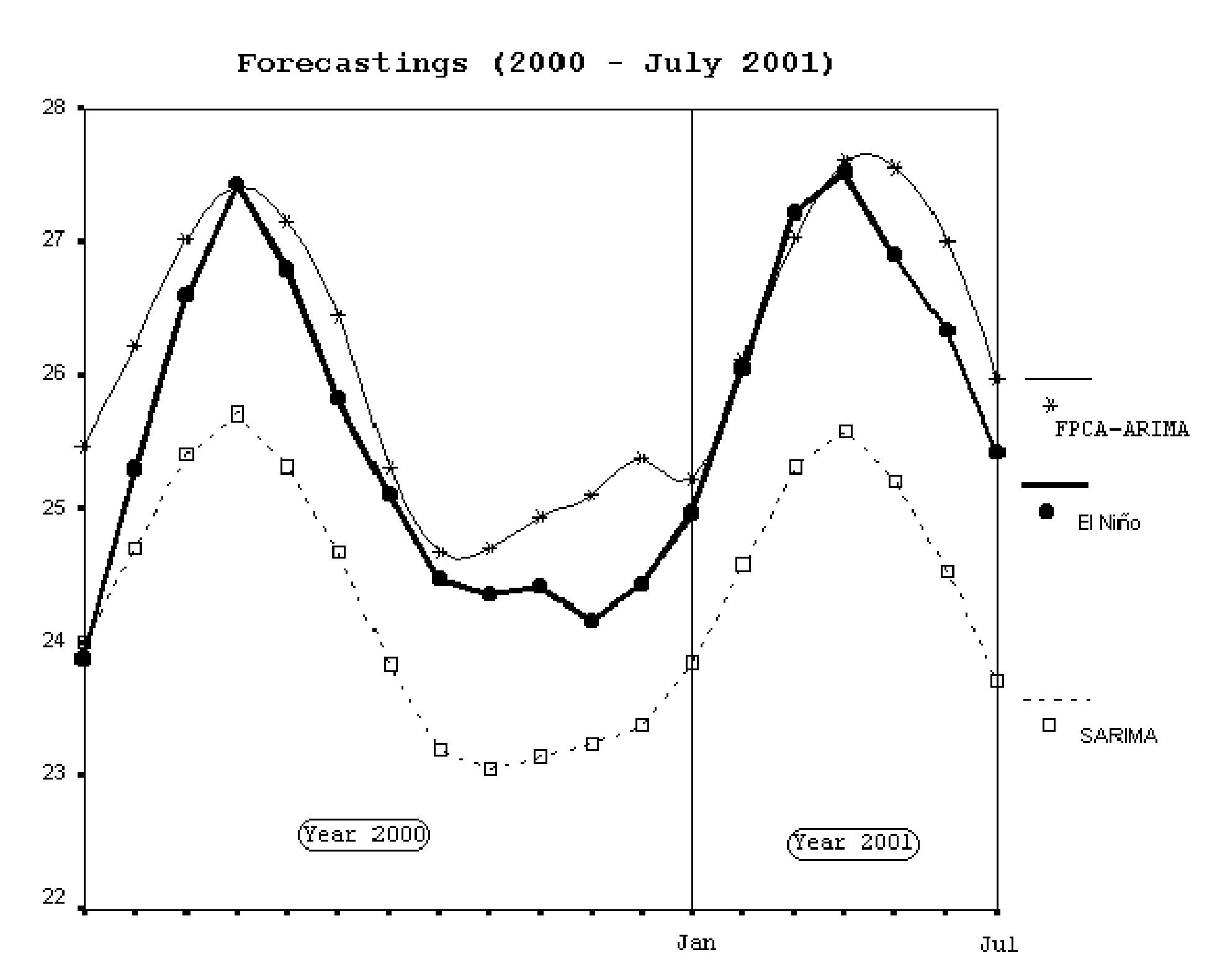
Estos problemas han planteado la necesidad de desarrollar metodologías potentes que permitan, en la práctica, la modelización y predicción a partir de datos funcionales dando lugar a una especialidad estadística muy reciente conocida con el nombre de Análisis de Datos Funcionales (FDA), que en la actualidad está siendo objeto de un estudio intensivo por parte de los investigadores. Los primeros trabajos en FDA estuvieron dedicados a la generalización de la técnica de reducción de dimensión Análisis en Componentes Principales (ACP) al caso funcional. Posteriormente las investigaciones en FDA se han centrado en el desarrollo de modelos de regresión funcional  y sus aplicaciones en diferentes campos como la economía, el medioambiente o las ciencias de la salud.

• Conocer las nociones básicas sobre variables funcionales (procesos estocásticos) de segundo orden.
• Manejar los métodos matemáticos de aproximación de funciones de cuadrado integrable (interpolación, aproximación mínimo cuadrática, …) a partir de bases de funciones (trigonométricas, splines, wavelets, ..).
• Estudiar la técnica de reducción de dimensión Análisis en Componentes Principales Funcional (ACPF) y métodos de estimación a partir de observaciones en tiempo discreto de las funciones muestrales.
• Conocer la formulación, estimación muestral e implementación computacional, así como la aplicación con datos reales e interpretación de resultados, de modelos de predicción en componentes principales (PCP) de una variable funcional.
• Relacionar los modelos PCP con los modelos más generales de regresión lineal funcional.
• Conocer la formulación, estimación muestral e implementación computacional, así como la aplicación con datos reales e interpretación de resultados, de modelos de regresión logística para estimar una variable binaria a partir de un predictor funcional relacionado.